2021年年底，医咖会“临床研究100问”正式启动。第一期直播，医咖会的老朋友李延龙带来了正态分布和正态检验中的常见问题，例如，K-S和S-W的结果不一致，怎么办？明明直方图显示分布很对称，但正态性检验认为不服从正态分布，怎么办？下文小咖将对相关内容进行简要整理，希望对大家有所帮助。

正态分布的应用场景

估计频数分布：对于正态分布的变量，只要知道均数与标准差，就可根据公式估计任意取值范围内频数比例。

制定参考值范围：正态分布法，适用于服从正态、或近似正态或转换后正态分布的指标。百分位数法常用于偏态分布的指标。

统计方法的理论基础：t检验、方差分析、Pearson相关、线性回归分析。

判断正态分布的三大法宝

正态性判断方法1：偏度和峰度

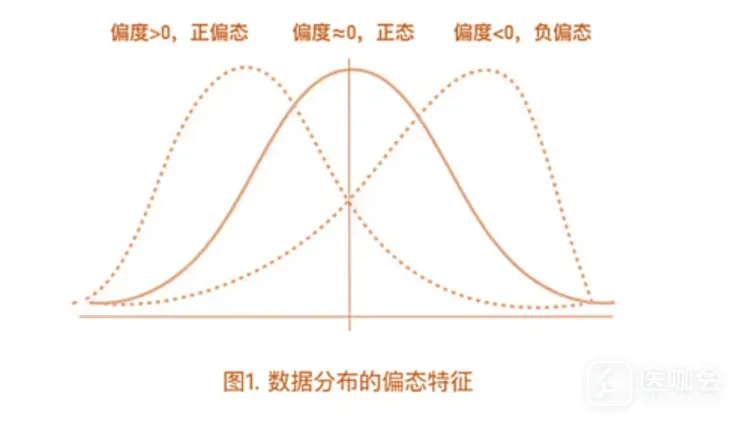
鉴于正态分布为倒钟型，因此两个指标可以用来刻画数据分布情况，即偏度和峰度。偏度（Skewness）：描述数据分布不对称的方向及其程度（见下图）。当偏度>0时，分布为右偏，也称为正偏态；当偏度<0时，分布为左偏，也称为负偏态。特别需要注意，数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置。

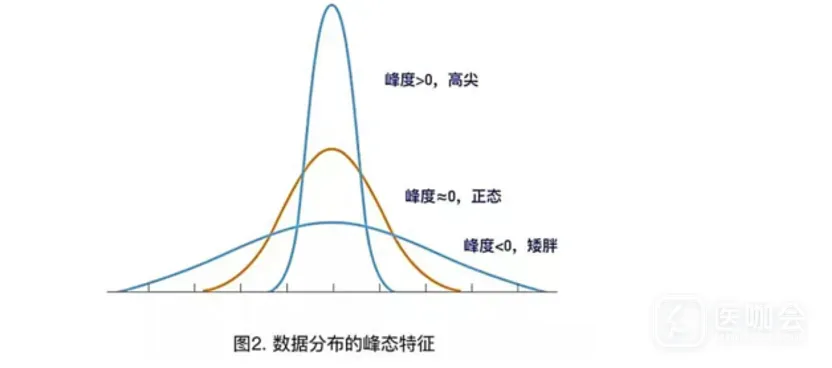
峰度（Kurtosis）：描述数据分布形态的陡缓程度（见下图）。当峰度≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；当峰度>0时，分布的峰态陡峭（高尖）；当峰度<0时，分布的峰态平缓（矮胖）。

利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score），即：偏度Z-score=偏度值/标准误，峰度Z-score=峰度值/标准误。在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为资料服从正态分布。

正态性判断方法2：图形判断

直方图、概率图和分位数图都可以直观地看出是否是正态分布，具体见下图。直方图表示连续性变量的频数分布，可以用来考察分布是否服从正态分布。服从正态分布时，图形为倒钟型，如下所示。