当结局为连续性变量时，我们通常认为干预效应是线性的，即干预组结局减去对照组结局，对应的模型则是一般线性模型。而当结局是其它变量类型时，例如二分类、多分类、计数、生存等等，此时并不能直接认为干预效应也符合线性（并非不能计算，而是我们需要更贴近现实的结果），因此需要做一些数据变换，使得干预效应变为近似线性关系，然后再进行线性运算。这种通过变换数据后线性近似的方法也被称为广义线性模型。

Meta分析的统一框架

同样的，广义线性模型也为Meta分析提供了一个可以应对各种类型结局的统一框架，在一般pairwise Meta分析中，频率学方法既可以选择一些非参数方法，如M-H法、倒方差法、Peto法等，也可以选择模型法，即广义线性模型，然后通过最大似然法进行估计。当在网状Meta中，频率学方法需要基于每个研究的干预效应进行建模，即网状结构矩阵和干预效应向量相乘，然后通过加权最小二乘和矩阵广义逆进行求解，而不同类型结局的效应是在建模前就计算好的，即研究内效应。因此在频率学中，并不存在真正的统一框架，而这一点可能正是贝叶斯方法的优势所在。

如前文所述，贝叶斯分析的优势之一则是基于臂进行建模（arm-based model），因此建模的过程是在计算干预效应前，即无需分两步先计算干预效应，而是直接对其进行建模，当配合马尔可夫蒙特卡洛算法（MCMC）时，可以使得建模过程变得非常简便。广义线性模型此时为贝叶斯Meta分析提供了统一的模型框架。

广义线性模型Meta分析由两部分基础组成：似然（likelihood）和连接函数（link function）。通常情况下似然由一些未知参数定义，而连接函数则是把这些参数映射至全体实数，此时干预效应可以假设为线性，即：

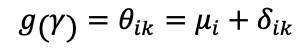
g即是连接函数，θ是第i个研究的第k臂的结局效应，μ则是第1臂（或对照组）自身的结局效应，同时也是我们不关心的冗余参数（nuisance parameter）。我们核心关注的参数是δ，即第k臂比第1臂的干预效应，也是待估计参数。对于随机效应模型，我们假设参数δ抽样于随机分布：

对于固定效应，方差设成0即可。