总的来说,使用均数±标准差描述正态分布或近似正态分布资料的基本特征;使用中位数与四分位数间距描述偏态分布或未知分布资料的基本特征。
对于连续变量,我们在描述数据分布时,有两类重要的指标:
- 集中趋势指标(反映所有观察值趋向的中心位置):如均数、中位数
- 离散趋势指标(反映所有观察值之间参差不齐的程度,即变异程度):如标准差、四分位数间距
具体选择何种指标来描述这两个维度,要取决于数据分布本身。对于正态分布,其为对称分布资料,均数位于分布的中心,可用于描述集中趋势。
而从标准差的公式不难看出,根号下的分子是每个观察值Xi与均数之间差值的平方和,利用了所有观察值信息,可用于描述变量的变异程度。故均数±标准差就能准确地刻画正态分布的分布形态。从图2可以看到均数增加时,分布整体右移;从图3可以看到从蓝色到黄色,标准差减小时,数据变异减小,数据更集中。正态分布也记作N(u,σ2)。
图1. 标准差公式



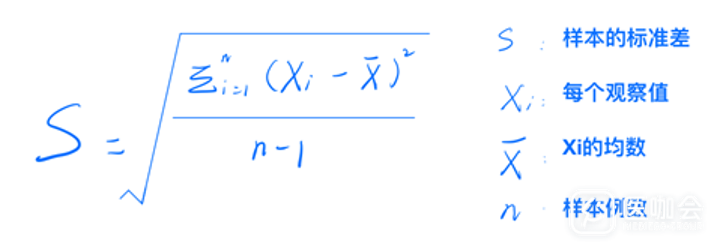











确认删除