问题1：相关与回归，我该选择哪个？

相关与回归都是分析变量间关系的方法，但不少人搞不清楚，我到底什么时候用相关，什么时候用回归。这个其实主要从研究目的来定，这两种方法侧重的研究目的不同。

相关（correlation）从字面意思就可以看出它描绘的是变量间的“相互”关系，即两个或多个变量不区分主次关系，重在解释变量间的关联。

而回归分析中的变量地位不同，有主次之分，注意力集中在其中的一个或几个自变量对因变量的影响，而不是因变量对自变量的影响。

在有的结构很清楚的软件中，如JMP软件，是将相关置于“多元分析”的菜单下，为什么呢？因为相关分析中，所有变量都是结果，没有原因，就是看这些变量之间的相互关系。

而回归分析则不是，只有一个结果，其它都是原因（注意这里的原因不是从时间上或因果关系上所谓的那个原因，只是为了说明问题，不是很严谨）。比如分析高血压的影响因素，高血压可以看做结果，而性别、年龄等因素可以看做原因。因为你想看的是性别、年龄等对高血压的影响，而不想反过来看高血压对年龄的影响。这就是回归分析。

问题2：没有线性相关就说明没有关系？

一般而言，我们所说的相关都是指线性相关，但这只是一般情况，而不是所有情况。比如，Pearson相关系数（主要用于正态分布数据之间的相关）和Spearman相关系数（主要用于非正态分布的数据之间的相关），这两个相关系数主要是用于线性相关的关联性度量，但是如果相关系数=0.1，并不代表说就没有相关。此时结论只能说无“线性相关”，但不能说没有“相关性”。

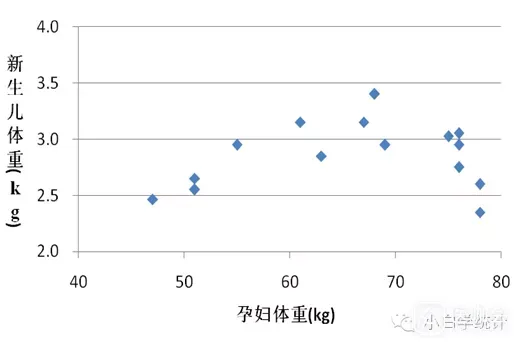
因为变量之间不仅是线性相关，也可能是曲线相关，变量之间的关系不一定是直线关系，更多的可能是曲线的关系。事实上，现实中有很多现象都不是线性的，而是非线性的。比如下图就是非线性的相关：

对于非线性的相关，如果还用Pearson相关，肯定是得不出想要的结果的，此时需要考虑曲线相关。

如何看变量间到底是线性相关还是曲线相关，最简单的方法就是通过绘制散点图来看 。如果散点图大致呈直线，那就是线性相关，如果呈指数形状、抛物线形状等，则最好先将变量进行变换，如对数变换、指数变换、平方、平方根变换等。将变换后的数据再进行直线相关分析。