作为一个临床研究工作者,在日常分析数据过程中,我们大量地使用Cox比例风险模型,却往往忽略Cox比例风险模型的一个重要假设-PH假设。这就导致我们在投文章的时候,审稿人经常会要求文章中补充如何判断PH假设的部分。
笔者就曾经遇到过这样的问题,被审稿人要求增加PH假设的判断。审稿人的comments如下:
The assumption for the proportional hazards model might have been violated, as seen in Figure 4 where the KM curves crossed each other, So a single summary measure using a proportional hazards model might not be appropriate.
所以本期我们将从三个方面展开,力图一次性地解决PH假设的相关问题,首先介绍什么是PH假设,然后介绍PH假设的判断方法,最后介绍PH假设不满足时该如何处理。
本文尽量使用通俗的语言来说明PH假设的问题,但是还是会保留一定的数学公式,供想深入了解的读者学习,只是想在自己文章中解决PH假设问题的读者可以跳过这些公式。
什么是PH假设
PH假设,即 proportional hazard assumption,指的是在使用Cox比例风险模型处理数据时,干预组与对照组的风险比(hazard ratio)在整个随访期间为常数,不随随访时间的变化而变化。(这里进行了简化处理,因为在投文章的时候reviewer主要关注的就是对于treatment来说PH假设是否成立,其实应该是所有纳入Cox模型的协变量都要满足PH假设)
Cox回归模型如下:
从上面的式子可以看出,当X1,...,Xk一定时,treatment等于1时的hazard为
treatment等于0时的hazard为
同理,对于其他协变量X1,...,Xk也一样。
PH假设的判断方法
PH假设的判断方法有两种:一种是基于回归方程的,一种是基于残差的。
R代码如下:
# cox model
res <- coxph(Surv(tstop, status) ~ treatment + X1 + X2 + X3, dta)
summary(res)
# cox model with treatment * time interaction
## f(t) = t
res.t <- coxph(Surv(tstop, status) ~ treatment + X1 + X2 + X3 + tt(treatment), dta,
tt = function(x, t, ...) x * t)
summary(res.t)
## f(t) = log(t)
res.logt <- coxph(Surv(tstop, status) ~ treatment + X1 + X2 + X3 + tt(treatment), dta,
tt = function(x, t, ...) x * log(t))
summary(res.logt)
注意,res.t <- coxph(Surv(tstop, status) ~ treatment + X1 + X2 + X3 + treatment * t, dta)是错误的,R也会给出如下错误信息:
Error in model.frame.default(formula = Surv(tstop, status) ~ treatment + :
参数't'的种类(closure)不对
2)基于残差的,Cox模型中用来判断PH假设的残差为Schoenfeld residual。
R代码如下:
# Schoenfeld residual test
## f(t) = t
cox.zph(res, transform = 'identity')
## f(t) = log(t)
cox.zph(res, transform = log)
所以,在实际数据分析过程中还要结合图示法对PH假设进行判断。
R代码如下:
# cumulative incidence plot
plot(survfit(Surv(tstop, status) ~ treatment, data=dta), fun = 'F', conf.int = T,
xlab = 'Days',
ylab = 'Cumulative Incidence', col = c('red', 'blue'))
R代码如下:
# log cumulative hazard plot
plot(survfit(coxph(Surv(tstop, status) ~ X1 + X2 + X3 + strata(treatment), data = dta)),
fun = 'cloglog', conf.int = T,
xlab = 'Days',
ylab = 'Log Cumulative Hazard', col = c('red', 'blue')





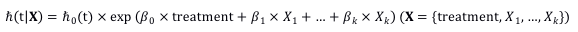
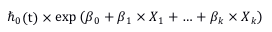
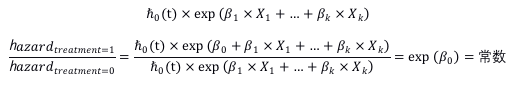
















确认删除