一、残差方差齐性判断

1. 残差方差齐性

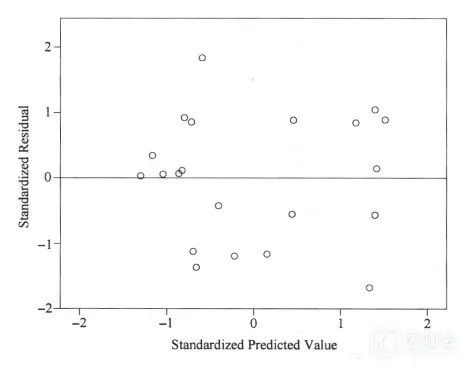
回顾一下前面介绍过的残差方差齐性，即残差ei的大小不随预测值水平的变化而变化。我们在进行残差分析时，可以通过绘制标准化残差和标准化预测值的散点图来进行判断。若残差满足方差齐性，则标准化残差的散点会在一定区域内，围绕标准化残差ei=0这条直线的上下两侧均匀分布，不随标准化预测值的变化而变化，如图1所示。

图1. 标准化残差散点图（方差齐性）

2. 残差方差不齐

但有时残差不满足方差齐性的假设，其标准化残差散点图显示，残差的变异程度随着变量取值水平的变化而发生变化，如图2(a)显示标准化残差的分布随变量取值的增大而呈现扩散趋势，图2(b)显示标准化残差的分布随变量取值的增大而呈现收敛趋势，说明残差不满足方差齐性的条件。

图2. 标准化残差散点图（方差不齐）

二、加权最小二乘法

在多重线性回归模型中，我们采用的是普通最小二乘法（Ordinary Least Square，OLS）来对参数进行估计，即要求每个观测点的实际值与预测值之间的残差平方和最小，对于模型中的每个观测点是同等看待的，残差满足方差齐性的假设。

但是在有些研究问题中，例如调查某种疾病的发病率，以地区为观测单位，很显然地区人数越多，所得到的率就越稳定，变异程度越小，而地区人数越少，所得到的率的变异就越大。在这种情况下，因变量的变异程度会随着自身数值或其他变量的变化而变化，残差不满足方差齐性的条件。此时如果继续采用OLS方法进行模型估计，则拟合结果就会受到变异程度较大的数据的影响，在这种情况下构建的回归模型就会发生偏差，预测精度降低，甚至预测功能失效。

为了解决这一问题，我们可以采用加权最小二乘法（Weighted Least Squares，WLS）的方法来进行模型估计，即在模型拟合时，根据数据变异程度的大小赋予不同的权重，对于变异程度较小、测量更精确的数据赋予较大的权重，对于变异程度较大、测量不稳定的数据赋予较小的权重，从而使得加权后回归直线的残差平方和最小，保证拟合的模型具有更好的预测价值。