统计分析一直以来都分为两个学派：频率和贝叶斯学派。它们最主要的区别就是关于被估参数的认知不同，频率学派认为被估参数是固定的，只不过观测实验有限，所以才会去计算假如进行无限次观测实验后的95%置信区间。

而贝叶斯学派认为真正的被估参数无法得到也不需要得到，我们只需要基于现有观测数据计算最接近真实情况的被估参数就可以了，因此被估参数是一个随机变量，我们直接计算它的概率分布。通常情况下这两类方法的选择没有优劣之分，但是在这里的网状Meta分析中，贝叶斯方法有一些独特的优势，比如灵活性高、天然的决策模型等等，因此本文主要介绍贝叶斯网状Meta分析模型。

核心模型框架

首先考虑Pairwise Meta分析，假设有M个试验，均为干预1对比干预2。此时，固定效应模型即假设每个试验i均为固定的效应量d12（即干预2相对于干预1的风险比OR或RR），不同试验中观测到的OR仅因随机误差的原因而不同，简而言之，研究间无效应修饰作用（即无异质性）。

然而，当存在明显异质性时，通常选用随机效应模型，即假设每个试验i产生一个效应量δi,12，表示为第i个研究中干预2比干预1的OR。随机模型中的效应量并不要求相等，但假设其满足可交换性，即效应量δ和试验标签i完全独立，也就是不同试验i中的效应量δi之间“可交换”(Bernardo and Smith, 1994)。这个假设也可以表示为效应量δi抽样自一个“公共”分布或“随机效应”分布。通常这个分布选择正态分布，即：

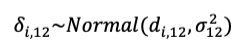
其中d12和σ12表示为正态分布的均值和标准差。当然，其他任何符合情况的分布都可以在这里使用。随机效应中的d12其实就是所有研究最终的合并效应量，也是我们所关注的、需要估计的核心参数。当标准差σ12=0时，模型退化为固定效应，此时δi,12=d12。

在贝叶斯框架中，参数估计可以额外施加一个先验分布，即估计前给定一些限制。然而，通常情况下，或在没有足够把握的情况下，我们希望最终估计值可以完全反应所纳入众多RCT的数据情况，因此会给定一些无信息或弱信息先验分布。

无信息的意思是先验分布可以覆盖任何可能的参数取值范围，例如我们想估计最终的合并效应量d12，在连续性分布尺度下（分类变量取对数即为连续性尺度），一个合理的可能是正无穷到负无穷，同时越偏离0点概率越小。因此，一个合适的无信息先验分布即为正态分布：

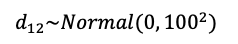
此外，对于研究间异质性参数σ12的先验分布则需要限制在所有正数之中，通常设定为均匀分布：

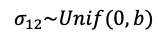
参数b为分布上限，需要根据具体效应量尺度决定。

具体实例

下面考虑一个假想的例子，假设一共有m个试验（i=1, 2, 3…, m），每个试验均为干预2对比干预1（或治疗组对比对照组）。在第i个试验中，设rik为事件发生数，nik为总人数，k为干预臂数（k=1为对照组，k=2为治疗组）。对于每个事件r只有发生、不发生两种可能，因此假设其满足二项分布：

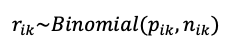
则pik为第i个试验第k臂中发生事件的概率（i=1,…,m; k=1, 2）。

此时数据为二分类变量（即只能取1发生；0不发生），因此在线性模型中需要变换为连续分布尺度（即取值范围由0、1变为全体实数）。通常我们选择使用logit函数将其映射至实数范围：

logit函数即为log odds函数，因此参数δi表示第i个试验中第k臂对比第1臂的logOR值（δi,12表示治疗组比对照组的logOR值），同时也是我们所关注的核心参数。δi,11表示为对照组比对照组的logOR值，设为δi,11=0（即效应相同）。因此完整的公式表示为：

对照组：

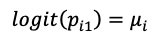
治疗组：

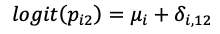
对于随机效应模型，logOR的参数δi,12=logit(pi2)−logit(pi1)取自随机效应分布。对于固定效应模型，δi,1k替换为di,1k且固定为常数（也可表示为随机效应分布方差等于0的情况）。

在模型中可以估计两个参数：对照组的log odds（即μ）、治疗组比对照组的logOR（即d或δ）。然而对于合并效应量，我们仅关注其中的logOR值，也就是治疗组比对照组的效应强度比。对照组单独的log odds并不是我们所关注的，属于冗余参数，通常给定一个无信息先验（即标准差100的正态分布）。

下面通过BUGS的代码展示一下固定效应模型的完整过程：

注意在BUGS的代码中，正态分布的参数指定为均值和精确值，精确值为方差的倒数，因此等于0.0001（即1/1002）。

最终我们关注的是d[2]的后验分布，分布的中位数即是治疗组比对照组的logOR，则exp(d[2])即等于OR值。

随机效应模型类似，但需要将d替换为δ，并且为其指定随机效应分布：

展示BUGS代码最主要的目的是后续说明间接比较和网状分析是如何在此框架下被直接拓展的。