Meta分析已经成为现在临床决策中非常关键的一部分，而网状Meta分析作为Meta分析的拓展，也在近些年被大力发展并应用于临床决策。为了区分，我们通常称传统Meta分析为pairwise Meta分析，其应用在仅有两种干预比较的情况下。而当干预超过两种时，pairwise Meta分析则不再适用，此时需要引入新的比较方法，即间接比较（indirect comparisons）。

1.间接比较和网状Meta分析

当我们有两对干预比较（A vs B、A vs C）的数据时，间接比较B vs C很自然的就产生了，表示为AB直接比较的结果（dAB）减去AC直接比较的结果（dAC），即

的确，我们可以通过AB、AC的数据来获得BC比较的数据，但这却不是最主要的目的。事实上，更多的情况是需要得到这三种干预中哪一个是最优的。而为了进行这些比较，我们需要一个假设，即不同试验中的效应量（如RR、RD等）在适合的尺度下必须相对稳定，尽管它们中每一组的response rate本身会变化。这是整个Meta分析中最基本的假设，也就是所谓“同质性假设”。

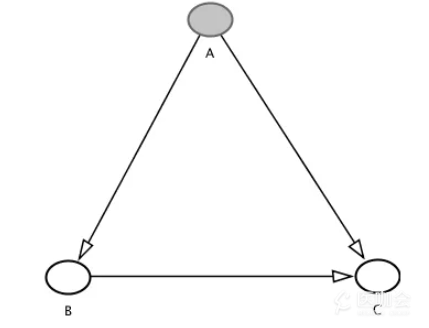
到此为止，我们进行的比较都非常简单，然而，当出现环路结构（loop）时，情况则变得复杂了一些。如图1中的闭合环路结构，假设我们有两个dBC的来源：（1）来自B vs C的直接比较数据，即关于BC的RCT，（2）来自AB、AC的间接比较数据。此时我们需要将dBC的两个来源数据合并，形成一个合并值。同时，我们也可以测试这两个来源数据即直接比较和间接比较的一致性。

图1

网状Meta分析的首要任务则是简单的将所有数据合并，通过某种“一致”的方式。那么什么是“一致”呢？回到图1中，假设现在分别进行3个不同的pairwise Meta分析，分别得到3个不同的结果：

然而，这三个结果并不能得到一个一致的决策来决定谁是最优的干预。一个简单的例子假设A、B、C三个人的体重比较为：A比B重2kg，B比C重3kg，那么我们应该得知A比C重5kg。然而此时我们又得知A比C仅重2kg，那么我们无法得出哪个人最重，因为出现了不一致。

同理，在刚刚3个分开的pairwise Meta分析中，我们需要的不是那3个直接比较的且不一致的结果，而是需要3个一致的估计，同时它们满足：

事实上，网状Meta分析即是一种“得到一致估计的方法”，因而得到一致的决策。在某种意义上，pairwise Meta分析和间接比较都是网状Meta分析的特殊例子。