想要了解样条回归，还是得先从直线回归讲起。

直线回归大家一般都知道是干什么的，用来描述两个变量的直线关系。比如下图，我们用一条直线描述身高和体重的关系。

直线回归很容易理解，也很容易解释，通常就是说，自变量x每增加1个单位，因变量y变化有多大。

如果现实中所有的现象都可以用直线回归，那就完美了。可惜的是，直线回归能用来描述的实际问题太少了，现实中绝大多数的关系都不是直线关系。这种情况下，就必须用其他的回归来拟合了。

直线回归比较常用的替代方法是多项式回归，事实上，直线回归也可以算是多项式回归的特例，也就是一次项。不过一般我们所说的“多”，都是指2个以上，所以一般把直线回归和多项式回归分开。

所谓的“项”，也就是我们在初中学到的次方，比如二次方、三次方。所以，直线回归，我们如果用公式来表示，那就是：y=a+bx

二次项回归，用公式表示，就是在直线回归的基础上，增加一个二次项：y=a+bx+bx2

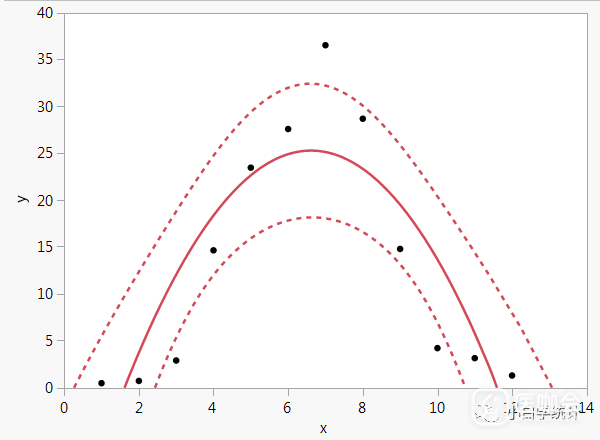
如果用图形来表示，二次项回归，就是曲线拐了一个弯，就像下面这个图：

对于这种非直线的点，你如果强行用直线回归，结果会让你很失望（当然，实际数据往往没有这么明显，很多时候也许你并不经意间就把非线性的关系用直线回归给做了，甚至可能也发表文章了，更甚至审稿人也没看出来）。

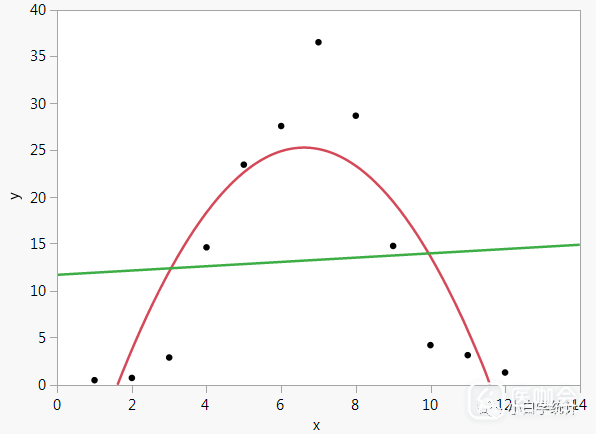
比如上面这个数据，如果你用直线回归，你会发现结果非常不靠谱（下图中的绿色直线），根本无法体现x和y的真正关系。

多项式回归可以在一定程度上很好地解决非直线的问题。古龙曾说过，没有什么数据是不能用一个3次项来解决的，如果有，那就用4次项、5次项、6次项、……（原话可能说的是酒）。总之，只要你的项数足够多，一定能完美拟合数据。