Meta分析的历史最早可以追溯到1925年Fisher先生的合并P值方法(Fisher's combined probability test)。也就是说,Meta分析其实是一个非常朴素的想法,即:当我们针对同一个假设做了多个独立的研究时,自然想得到一个最终的结果作为判断依据,而我们希望这个结果能比其中任意一个单独的结果更接近真值。
那么,所面临的第一个问题,也是最本质的问题,即是:为什么针对同一个假设的不同研究结果会有所不同?或者更进一步,我们针对同一个假设做了多个理想的RCT研究(假设不存在依从性问题和失访问题),而众所周知,RCT的结果是不存在偏倚的,所以结果理应都是真实无偏的,那么为什么结果仍然会有区别?我相信大家的第一反应都是:当然是因为随机误差的存在。因为我们每一个RCT的研究样本均假设为从某个目标总体随机抽样而来,也就是说如果研究使用无偏一致的估计量,那么得到的效应量与真值之间的差别则仅仅是因为随机所致,而随着样本量的增加,效应量会一致收敛于真值。
知道问题的答案,下一步就简单了,不同RCT因为样本量的区别,所以估计的精确度不同,精确度高的研究的效应量理应有更高的价值。因此,一个很自然的Meta分析步骤即是给每一个RCT的效应量赋予一个权重,精确度高的效应量权重大,精确度低的权重小。而通常情况下,精确度是通过方差来衡量,方差大的精确度低所以权重小,因此,我们只需要取方差的倒数作为效应量的权重,算一个加权平均效应量即可:
当效应量取OR时,这个方法退化为Mantel-Haenszel estimator,此时权重为:
当权重仅取“倒方差”时,模型称为固定效应模型,意为仅取研究内方差作为权重。而当权重同时考虑研究内方差和研究间方差时,则变为随机效应模型,等同于随机效应方差分析模型,即:





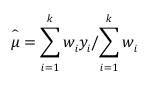
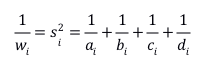












确认删除