作者:李侗桐;审稿:张耀文
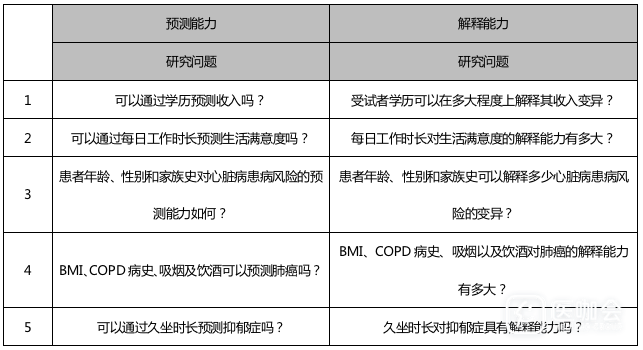
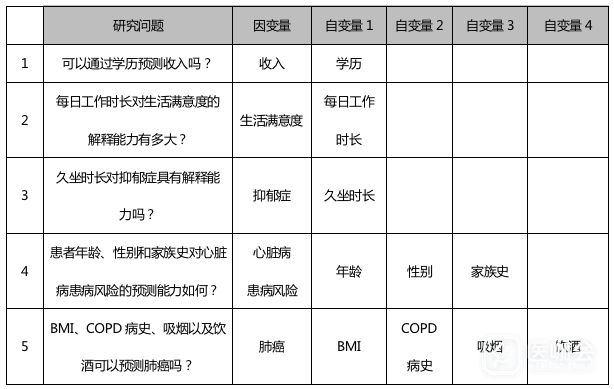
预测模型是基于变量之间的相关关系,通过一个或几个变量预测另一个变量的分析方法。我们可以根据自变量(预测变量或解释变量)预测因变量(应答变量或结局变量)。比如,通过久坐时长预测受试者的血液胆固醇浓度,或者根据受试者的年龄、性别、BMI等变量信息预测高血压病发病情况。此外,预测模型还可以帮助我们判断各自变量的重要性,即自变量对因变量的解释能力。举例来说,预测模型可以用来分析学历对收入的解释程度。示例如下:
1 连续变量
确定因变量是连续变量后,我们需要判断自变量的数量,示例如下:
1.1 只有一个自变量
简单线性回归。该检验可以基于一个连续型自变量对相应的连续型因变量进行预测,也可以评价自变量对因变量的解释力度。
1.2 包含多个自变量
多重线性回归。该检验可以通过多个自变量对相应的连续型因变量进行预测,也可以评价自变量对因变量的解释力度。
2 计数变量
泊松回归。该检验适用于分析因变量是计数变量的多因素预测模型。
注:计数变量是一个非负整数。比如,0、5、16、27是计数变量,但是2.7、5.8、18.2不是,因为它们不是整数;-2、-7、-15也不是,因为它们小于0。
计数变量不属于我们常用的变量分类,常被视为连续变量纳入分析。当计数变量比较大,多数数值超过40时,我们可以将其作为连续变量。但是当计数变量比较小,如多数数值小于10时,我们建议保留其计数变量属性,避免统计偏倚。计数变量示例如下:
a.菌群数量,培养基暴露24小时后可观察到的菌群数量
b.死亡人数,队列中每年因吸烟死于肺癌的人数
c.癫痫发作次数,受试者在一周内的癫痫发作次数


















确认删除