作者:李侗桐;审稿:张耀文
上节课程中,我们讲解了两个变量的相关性分析时,应该如何选择统计方法(详见:要做相关性分析,该如何选择正确的统计方法?),今天我们接着讲解,涉及到三个及以上变量的相关性分析,该如何选择统计方法。
分析三个及以上变量的相关性时,我们的主要目的是分析两个“主要”观察变量的相关性,并考虑其它因素对其关联的影响,这就需要纳入其它因素。以三个变量为例,我们拟研究变量A和变量B之间的相关性,但希望“去掉”或“校正”变量C的影响,即分析调整变量C后,变量A和变量B的关系。在这种情况下,我们就需要在该研究中纳入变量C。
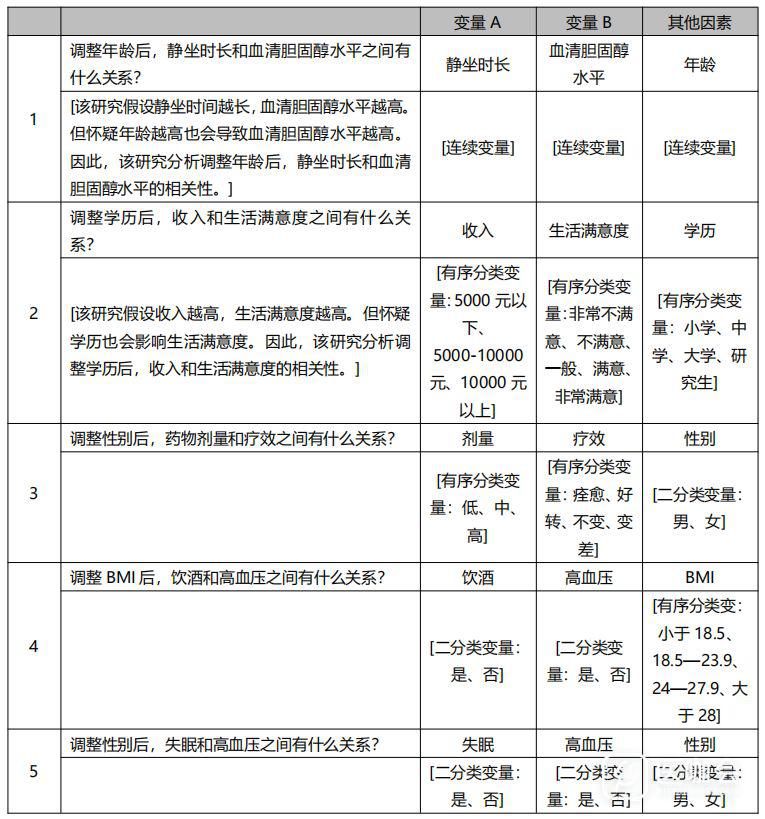
纳入其它因素是为了去除该类因素对主要观察变量相关性的影响。调整该类因素后,可以减少其对研究结果的干扰,更加准确地分析两个主要观察变量之间的关联,保证结果的真实可靠性。示例如下:
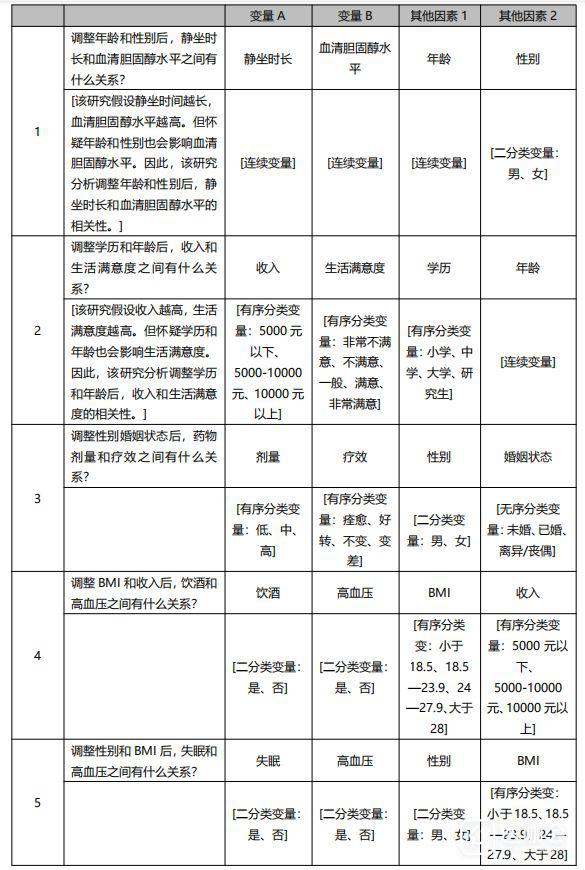
同样的例子也适用于分析含有4个或更多变量的相关性分析中,两个主要观察变量不变,但需要控制因素的数量增加,示例如下:
统计方法选择
① 纳入其它连续变量
Pearson偏相关。Pearson偏相关适用于分析两个连续变量的相关性,可以纳入其他连续变量。该检验不区分自变量和因变量,是Pearson相关中包含2个以上连续变量的特殊类型,不仅可以提示偏相关的统计学意义,而且可以通过相关系数提示关联强度。
② 纳入其它任意类型变量
多重线性回归。如果想区分自变量和因变量,可以采用多重线性回归进行分析。该检验不仅可以反映相关性,而且可以根据自变量预测因变量。需要注意的是,无序多分类的自变量需要做哑变量处理。有序分类变量如果不是定距的,也需要做哑变量处理。
1.2 两个主要观察变量均为分类变量


















确认删除