作者：张耀文

经常有小朋友问我：区间估计的95%可信区间（95%CI）和假设检验的P值是等价的吗？更具体的问法是：两组均数的95%CI重叠，t检验的P值一定大于0.05吗？

答案是：不一定。如果两组均数的95%CI不重叠，t检验的P值一定小于0.05；但如果两组均数的95%CI重叠，t检验的P值可能大于0.05，也可能小于0.05。

这是为什么呢？

由于t检验需要考虑方差齐性的问题，计算公式比较复杂，且当n足够大时，t分布趋近标准正态分布。我们这里以符合标准正态分布的Z检验来解释上述问题（如果使用t检验的公式，会比较复杂，但结果类似）。

1、Z检验的95%可信区间

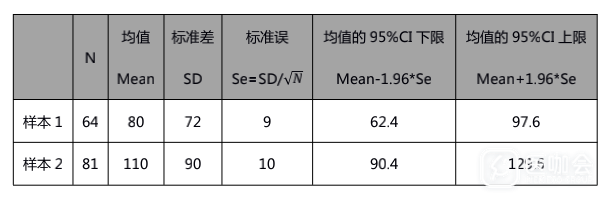
我们假设两个样本，N1=64，N2=81，其它参数如下表。

可以看到样本1的均数的95%CI为（62.4，97.6），样本2的均数95%CI为（90.4，129.6），两个95%CI重叠。

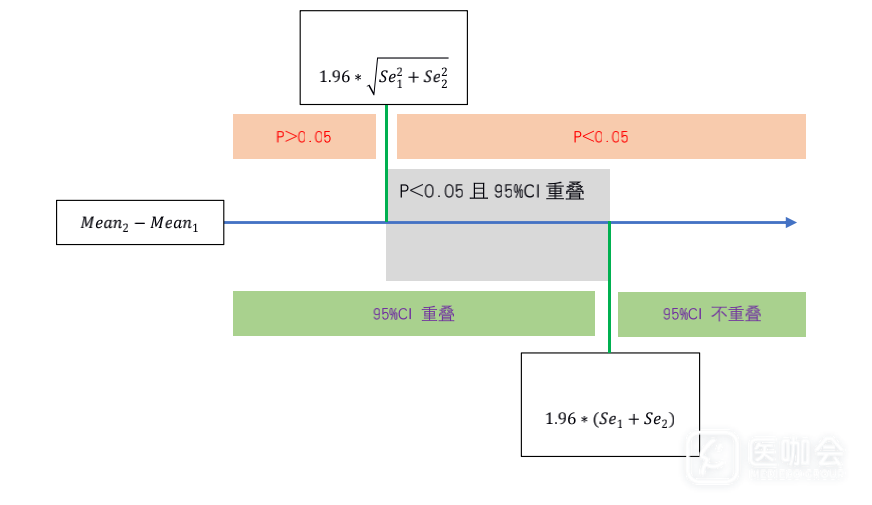
95%可信区间的估计公式是Mean±1.96*Se。则对于两个样本（假设样本1的均数较小），判断95%CI是否重叠，则需要判断样本1的95%CI上限是否大于样本2的95%CI下限，等价于判断Mean1+1.96*Se1-(Mean2-1.96*Se2) > 0 是否成立。即Mean2-Mean1<1.96*（Se1+Se2）时，95%CI重叠。

2、Z检验的P值

3、95%CI和P值的关系

实际上，上述的1.96，是标准正态分布Z0.05/2对应的界值，对应t分布自由度为无穷大的界值。如果使用t/t'检验，由于单个样本区间估计和两样本t/t'检验时自由度不同，检验界值会略有不同，情况比较复杂。

但结论是一样的，即：如果两组均数的95%CI不重叠，t检验的P值一定小于0.05；但如果两组均数的95%CI重叠，t检验的P值可能大于0.05，也可能小于0.05。