作者：张耀文

临床研究中，经常要计算某个样本的率（proportion），以及根据样本的率估算总体率的95%可信区间（Confidence Interval，CI）。样本率的计算很容易，那如何计算估算总体率的95%CI呢？

对于此类二项分布的数据，如果“数据量足够大”，一般可以使用正态近似法估算总体率的可信区间。

那如何才是“数据量足够大”呢？这个没有统一的标准。有学者推荐若以相对误差控制在10%左右为实际可接受标准，则使用正态近似法估计总体率95%可信区间的近似条件为 : 

1）当 n×p=5时，样本率应在40%-60%之间；

2）当 n×p=10时，样本率应在20%-80%之间；

3）当 n×p=15时，样本率应在1%-99%之间。由于1%-99%几乎包括了二项分布率的实际应用范围 ，且在此条件下的可信度与1-α水平相当 ，故n×p=15为应用近似法的“理想条件”[1]。

1、单个率及其95%CI

也可以使用各种软件计算率及95%CI，一个在线工具是VassarStats

（ http://vassarstats.net/index.html ）。

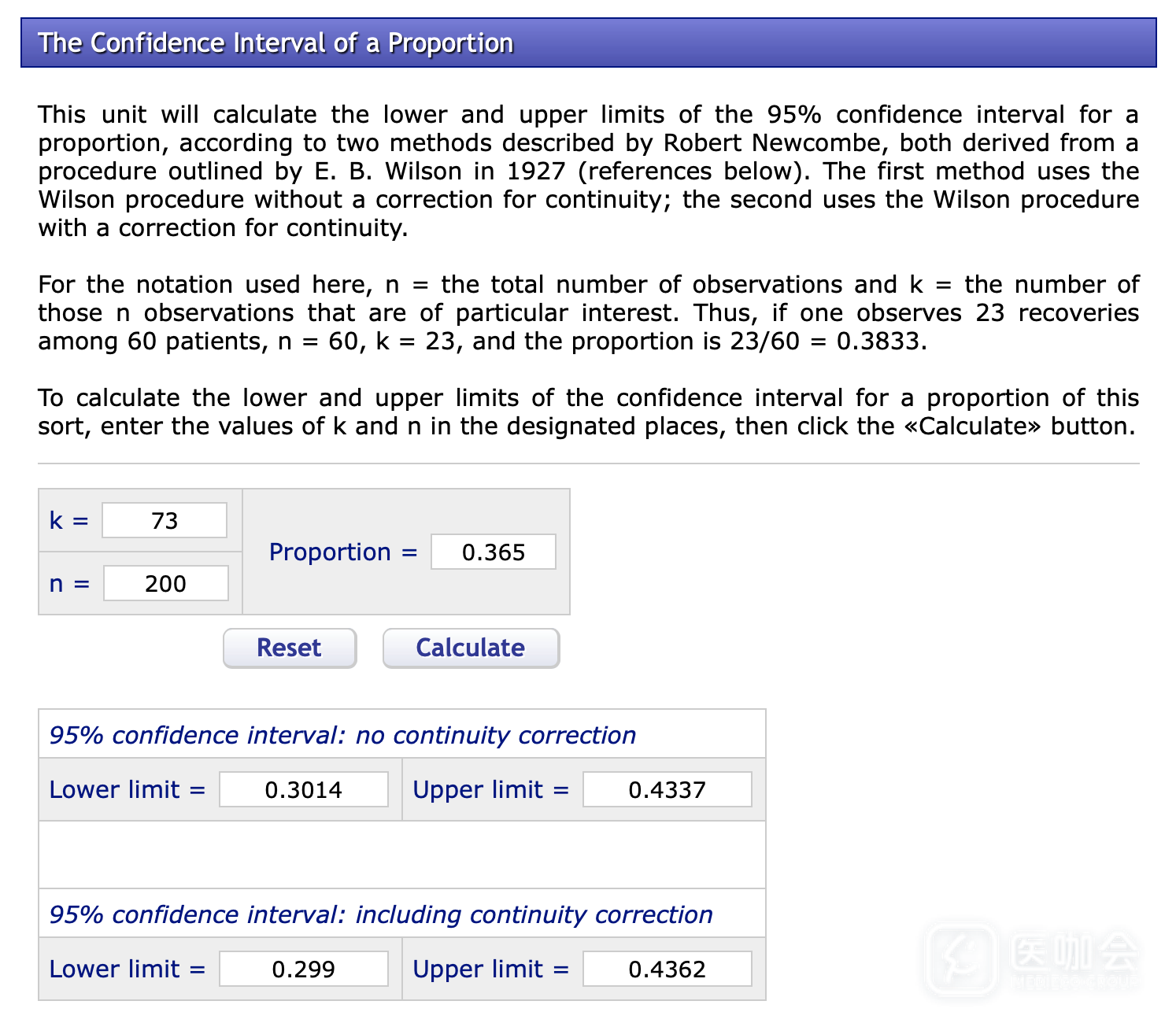
在VassarStats的主界面点击Proportions→The Confidence Interval of a Proportion即可计算。不同的是该在线工具使用不是正态近似法，而是Wilson法，同时与手工计算取舍小数点不同，所以计算结果略有差别。

2、两个率的差及率差的95%CI

使用VassarStats工具计算时，可在VassarStats的主界面点击Proportions→The Confidence Interval for the Difference Between Two Independent Proportions。