文章来源于“小白学统计”公众号,感谢作者授权
在医学杂志中,几乎绝大多数的生存曲线比较,都是用log-rank检验。根据我个人的审稿以及看到的文章情况,怎么也在98%以上。然而,log-rank检验并非生存曲线比较的万能法宝。事实上,在有些情况下,log-rank检验结果未必有效,或者说的严重一点,有可能是错误的,会给你误导。本文就说一下,log-rank检验到底在什么情况下失效?
首先,简单介绍一下log-rank检验。
log-rank检验,中文一般翻译为对数秩检验。常用于生存数据的组间比较。其基本原理大概是这样(以两组比较为例):
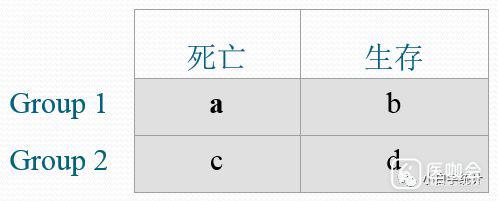
将两组非删失时间混合从小到大排序,得多个四格表,每个四格表如下:
然后计算公式如下(你肯定在想,为什么要介绍公式?我又不手动计算,看公式有什么用?但是,想要理解不同检验方法的区别,还真的得看看公司,当然,你不用了解太深入,大致明白什么意思即可):
这个公式是不是跟卡方检验的公式很像呢?其实这就是卡方,统计量就是卡方。只不过换了个应用场景而已。
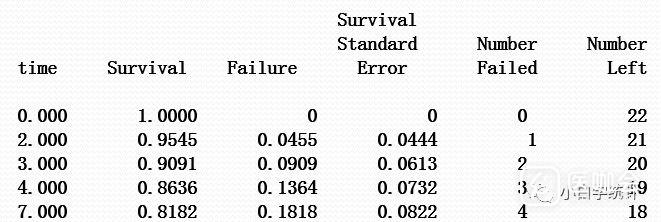
举例说一下,假设有两组数据,第一组(control)如下:
也就是说,在第2个月,死亡1例,总共22人剩了21人。
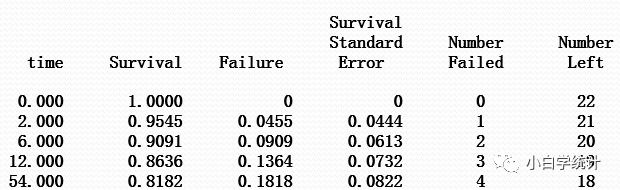
第二组(treated)如下:
也就是说,第二组人,在第2个月,死亡1例,总共22人剩了21人。
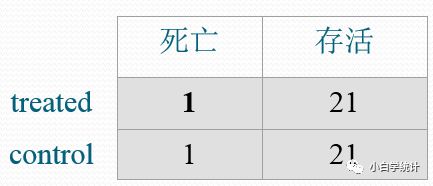
所以,在2个月这个时间点,两组情况是:
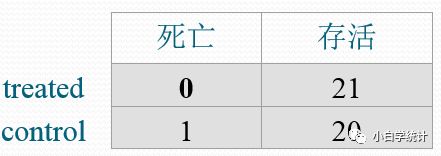
以此类推,就能得到,第3个月这个时间点,两组情况变成了:
一直往下计算,就能得到多个时间点的四格表,每个四格表就能根据上述公式计算,最后把多个时间点的求和,就得到了log-rank检验统计量。
其次,介绍一下Wilcoxon检验(Breslow检验)。
除了log-rank检验之外,还有一种比较常用的(而且大多数软件中都是和log-rank检验一起出现的)的方法是wilcoxon检验(spss中叫法是Breslow检验)。可能很多人都听过这个名字,可能会想,这不是秩和检验吗?其实统计学中经常有这种问题,在不同场合看到同样的名字(其实你在ROC曲线下面积的检验中依然能看到wilcoxon检验的身影)。但往往并不是一回事。起码公式并不相同。



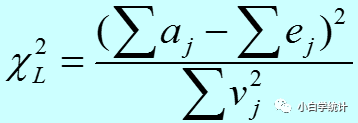












确认删除