文章转载自“小白学统计”公众号，感谢作者授权。

不少人曾问我：我的数据中有异常值，是不是应该删除？要回答这个问题，我们必须从异常值的概念来谈起。可能有的人觉得异常值很好理解，不就是“异常”的值吗？关键是，怎样才算异常呢？

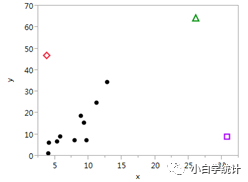
例：在10个数据中（下图黑色点）人为加入红、绿、紫色的3个点，它们都是异常值吗？

异常值其实是一个较为宽泛的概念，它至少包含了三种情形：

(1) 离群值（outliner）

离群值是指从因变量y的角度来看属于异常的值，如图中的红色点和绿色点，偏离y的均值较其它点更远。

离群值通常采用学生化残差来判断。

(2) 高杠杆值（high leverage）

高杠杆值是指从自变量x的角度来看属于异常的值，如图中的紫色点和绿色点，在x轴上偏离x的均值较远。

高杠杆值通常采用杠杆值来判断。

(3) 强影响值（influential observation）

强影响值是指对模型影响较大的值，也就是说，如果删除了该值，会导致模型发生很大变化（如系数值改变较大）。

强影响点通常采用COOK'D值、DFBETAS和DFFITS来判断。

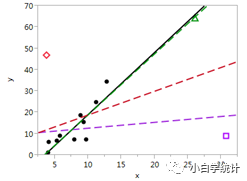
下图比较了不同异常值对模型拟合效果的影响。图中黑色实线表示不含这3个异常值的拟合线，绿色、红色、紫色虚线分别表示含绿色点、红色点、紫色点时的拟合线。

不难看出，含有绿色点时，对模型拟合影响几乎不大（与黑色实线几乎重合）；含有紫色点时，拟合线被向下拉低，即回归系数远低于黑色实线；含有红色点时，拟合线也被拉低。

如果要判断的话，绿色点虽然从x方向和y方向上都偏离均值，但却不是强影响点；紫色点和红色点才是强影响点，因为单独的任一点便可以导致系数发生很大变化。