最近,小咖收到不少小伙伴们关于置信区间和p值的疑惑,今天就让我们通过几个例子,来剖析一下这两个统计指标的关联。
简单回顾一下重要的定义。置信区间(confidence interval,CI),常常和观测值的点估计值一起出现,是样本对总体的一个区间估计,也可以被看作是点估计值可信程度的一种体现。 p值是假设检验中的关键结果,从统计学的角度衡量了数据与假设之间的关系(可点击查看:你真的理解p值么?一句话解释p值的常见误解。。。),实际应用上,通过将p值和预先设定的临界值(通常会使用0.05)做比较,我们可以判断统计结果是否显著。
这两个看起来不是很相关的数据,其实有着千丝万缕的关系。因为置信区间的计算方法,有时通过观察置信区间的范围,也能得出和p值相同的结论。从下面的例子出发,我们能从统计学的角度深入理解它们的关系。
1. 单个样本与总体比较
单个样本分析的假设检验中,我们通常会有一个假设值。譬如,已知某市初中女生的平均身高为156.7cm,某学校想要知道本校初中女生的平均身高是否和全市水平相同,这就是一个双向的假设检验,即检验“该校初中女生身高是否等于156.7cm”,这一假设。学校随机抽取了30(n)名初中女生测量身高,计算出平均身高156.46cm,标准误1.09cm(S/√n),根据置信区间的计算公式:
我们可以计算出95%置信区间(144.25,168.67),观察到这个区间包括了一开始的假设值(μ),156.7cm。
那么,假设检验中会发生什么呢?在双向假设检验中,我们首先根据下面的公式计算统计量:
然后再将得到的t值与t分布比较,得到p值=0.83,没有统计差异。







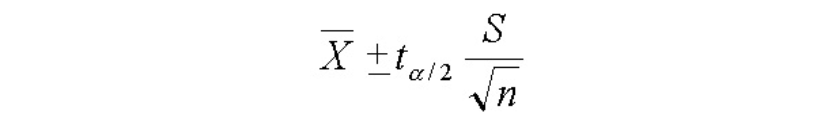
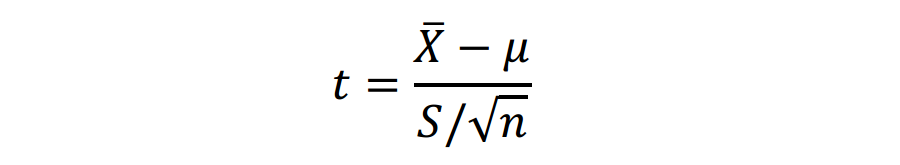











确认删除