一、问题与数据
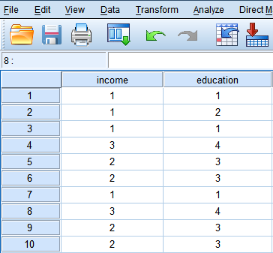
某研究者开展了一项关于学历和收入水平的调查研究。研究者收集了研究对象的学历,变量名为education,分为4组(1-初中及以下,2-高中,3-本科,4-研究生及以上),同时也调查了研究对象的收入情况,变量名为income,分为3组(1-低收入、2-中等收入,3-高收入)。研究者想探讨两个有序分类变量education和income之间是否存在相关性以及相关的方向。部分数据图1。
图1 部分数据
二、对问题分析
要判断两个有序分类变量之间是否存在相关,建议使用Kendall’s tau-b相关分析,但需要先满足3项假设:
假设1:两个变量是连续变量或有序分类变量,可以有三种情况:①两个连续变量;②两个有序分类变量;③一个有序分类变量,一个连续变量。
假设2:两个变量应当是配对的,即来源于同一个个体。
本例中,两个变量education和income都是等级变量,符合假设1;两个变量均对应同一研究对象,符合假设2。
扩展阅读
两个连续变量间呈线性相关时,可以使用Pearson相关系数,不满足Pearson相关分析的适用条件时,可以使用Spearman相关系数来描述。
Spearman相关系数又称秩相关系数,是对两变量的秩次大小作线性相关分析,对原始变量的分布不作要求,属于非参数统计方法,适用范围要广些。对于服从Pearson相关的数据亦可计算Spearman相关系数,但统计效能要低一些。
Kendall's tau-b等级相关系数适用于两个分类变量均为有序分类的情况(也可以用于有序分类变量+连续变量或两个连续变量)。
Kendall's tau是由英国统计学家Maurice George Kendall爵士于1938年提出。Kendall's tau秩相关系数包括一组评价系数:Somers' D、Goodman-Kruskal's gamma(γ)、Kendall's tau(a、b、c),其中较常用的是Kendall's tau-b和Kendall's tau-c。一般认为,tau-b更适合正方形表格(即行和列的数量相同),tau-c更适合长方形表格,但用tau-b来分析长方形表格也比较常见。





















确认删除