当我们应用统计方法对数据进行分析时，会发现许多计量资料的分析方法，例如常用的T检验、方差分析、相关分析以及线性回归等等，都要求数据服从正态分布或者近似正态分布，但这一前提条件往往被使用者所忽略。因此为了保证数据满足上述统计方法的应用条件，对原始数据进行正态性检验是十分必要的，这一节内容我们主要向大家介绍如何对数据资料进行正态性检验。

一、正态性检验：偏度和峰度

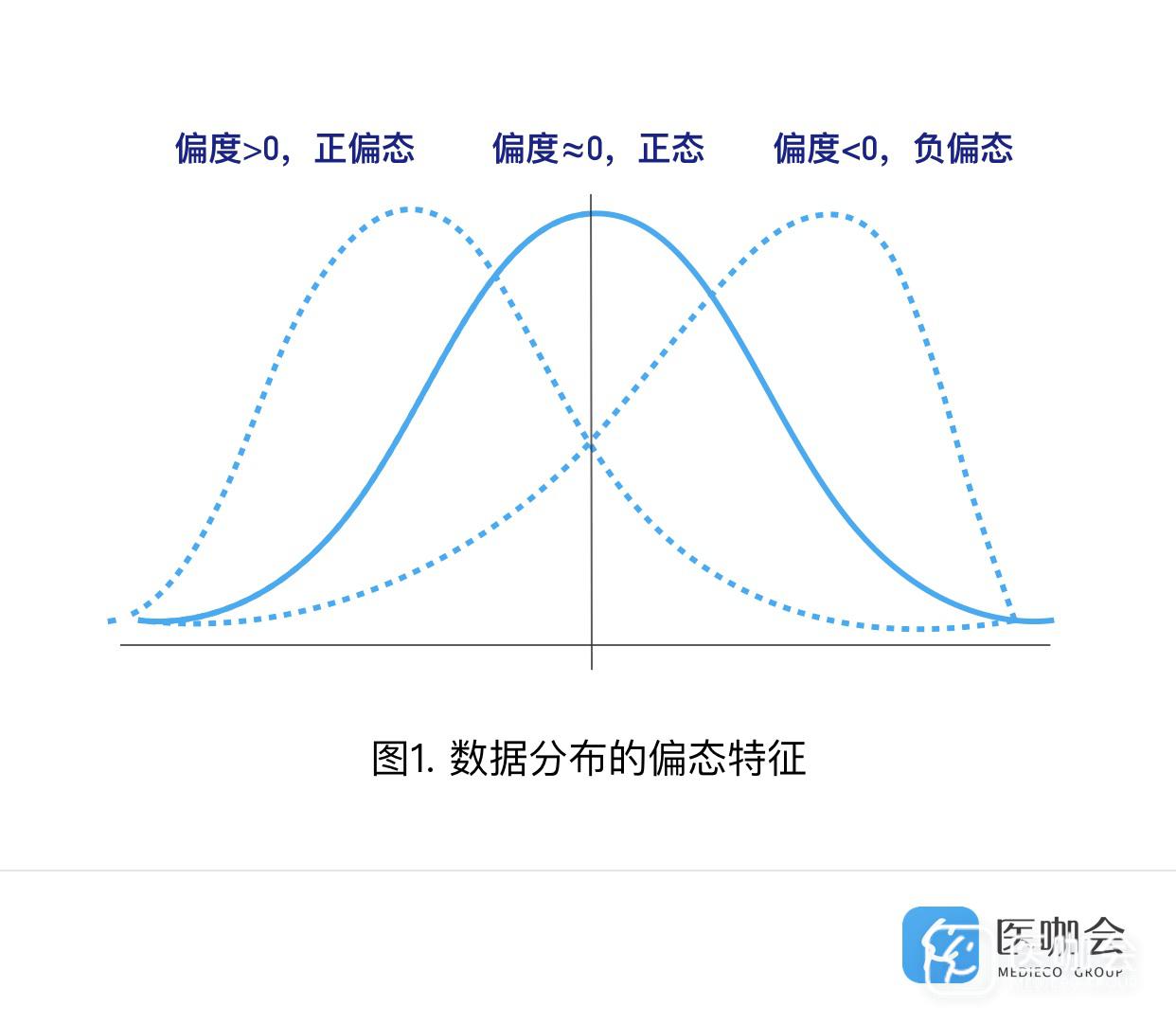
1、偏度（Skewness）：描述数据分布不对称的方向及其程度（见图1）。

当偏度≈0时，可认为分布是对称的，服从正态分布；

当偏度>0时，分布为右偏，即拖尾在右边，峰尖在左边，也称为正偏态；

当偏度<0时，分布为左偏，即拖尾在左边，峰尖在右边，也称为负偏态；

注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置，容易引起误解。

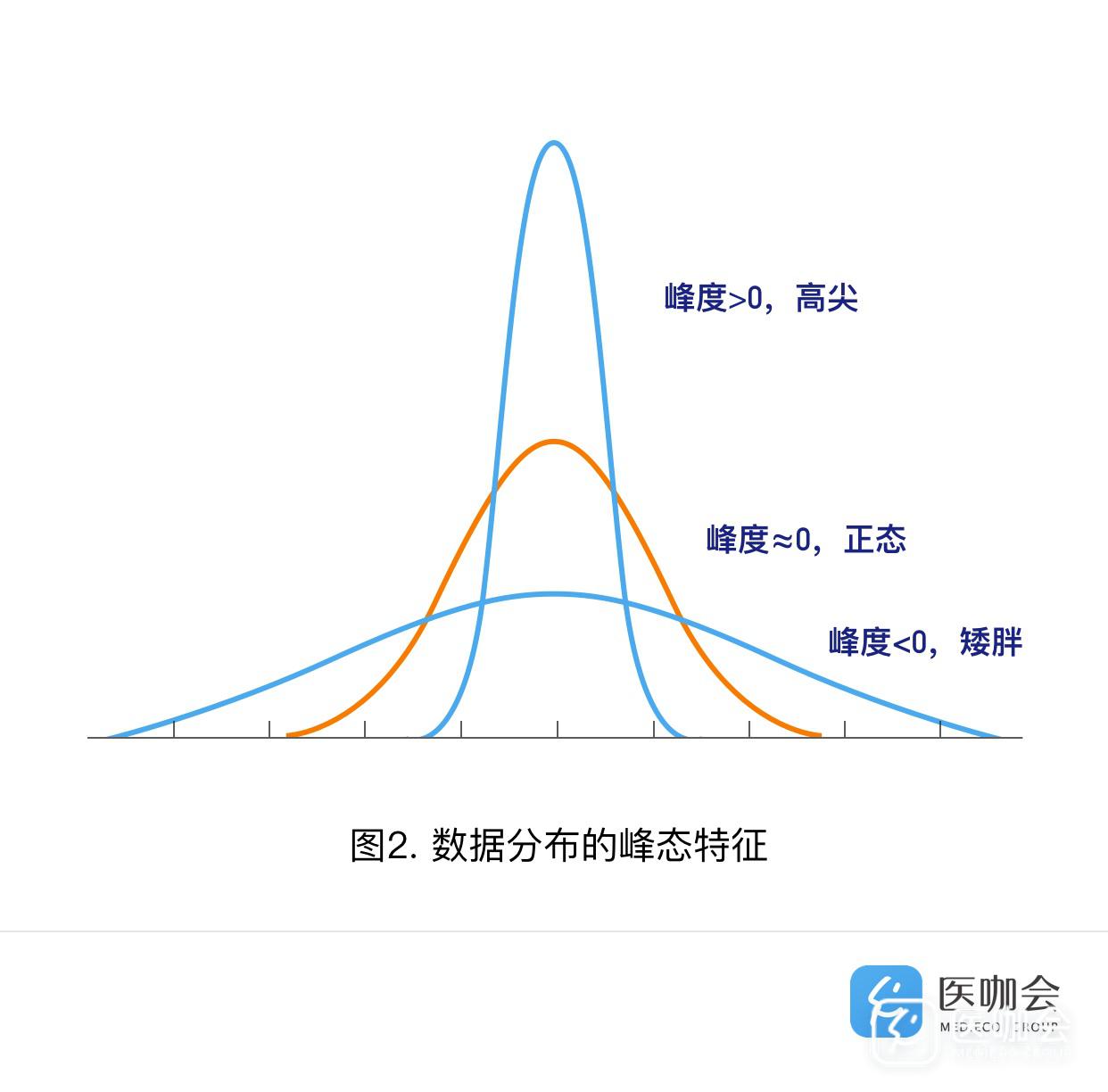
2、峰度（Kurtosis）：描述数据分布形态的陡缓程度（图2）。

当峰度≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；

当峰度>0时，分布的峰态陡峭（高尖）；

当峰度<0时，分布的峰态平缓（矮胖）；

利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score），即：偏度Z-score=偏度值/标准误，峰度Z-score=峰度值/标准误。在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为资料服从正态分布。

了解偏度和峰度这两个统计量的含义很重要，在对数据进行正态转换时，需要将其作为参考，选择合适的转换方法。

3、SPSS操作方法

以分析某人群BMI的分布特征为例。

(1) 方法一

选择Analyze → Descriptive Statistics → Frequencies