据说,每个人天生都是贝叶斯统计学家。
贝叶斯定理,听起来很遥不可及,其实贝叶斯定理应用在我们生活的方方面面,也包括医学研究当中。今天,我们就来认识一下贝叶斯定理,以及它在诊断试验中的应用。
一、贝叶斯定理
贝叶斯到底是指什么呢?举一个简单的例子。今天乌云密布,我要不要带雨伞出门?
为什么我们看到天上乌云密布,就觉得要下雨了呢?那是因为,根据经验,下雨之前往往乌云密布。
但是,“乌云密布”一定会“下雨”吗?未必。
有的时候,尽管天上有乌云,可是风一吹就吹散了。也有时候,天上下雨并没有乌云,而是隔壁老王她媳妇儿在倒洗脚水。那么我们如何知道,在乌云密布的时候,下雨的概率有多高呢?
以小咖所在的帝都为例,我们可以统计1年内乌云密布时下雨的次数,和乌云密布的次数。
在等式的右边,分子分母同时除以365,则得到:
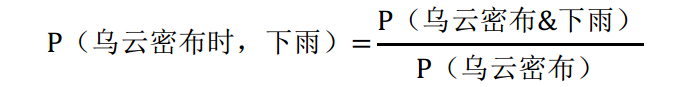
当然,有时候下雨也不一定就会乌云密布,有可能是隔壁老王她媳妇儿在倒洗脚水。帝都下雨的概率是:
假设帝都每年平均有60天下雨,则P(下雨)=60/365=16%。
显然,后者要小于前者。为什么都是下雨,两个概率不一样呢?
这是因为,前者在计算时,限定了“乌云密布”这个条件,我们把这种概率,称为条件概率。所谓条件概率,是指事件A在另外一个事件B已经发生条件下的发生概率,表示为:P(A|B)。上面的例子中,P(乌云密布时,下雨)可记为P(下雨|乌云密布)。
文章一开始,我们就断定“每个人天生都是贝叶斯统计学家”呢。为什么呢?
这是因为,我们每天出门时,判断要不要带伞,是先要看一下天气的。如果今天乌云密布,那么我们就判断今天下雨的概率——即P(下雨|乌云密布)比较大,需要带伞。如果今天没有云,我们可能也会带伞,但可能性不大,因为我们判断帝都下雨的平均概率只有16%。








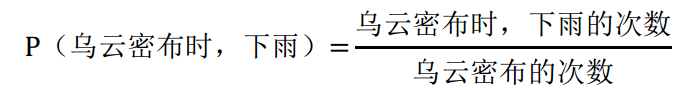












确认删除