一、问题与数据
在前边的文章我们分别介绍了两组比较的秩和检验与配对秩和检验,然而在研究中往往有多个独立样本需要进行比较,如果多个样本的观察值满足独立性,服从正态分布,并且各组之间的方差齐,则可选用单因素方差分析,如果样本数据不满足上述几个条件,则需要用到多个独立样本的秩和检验。
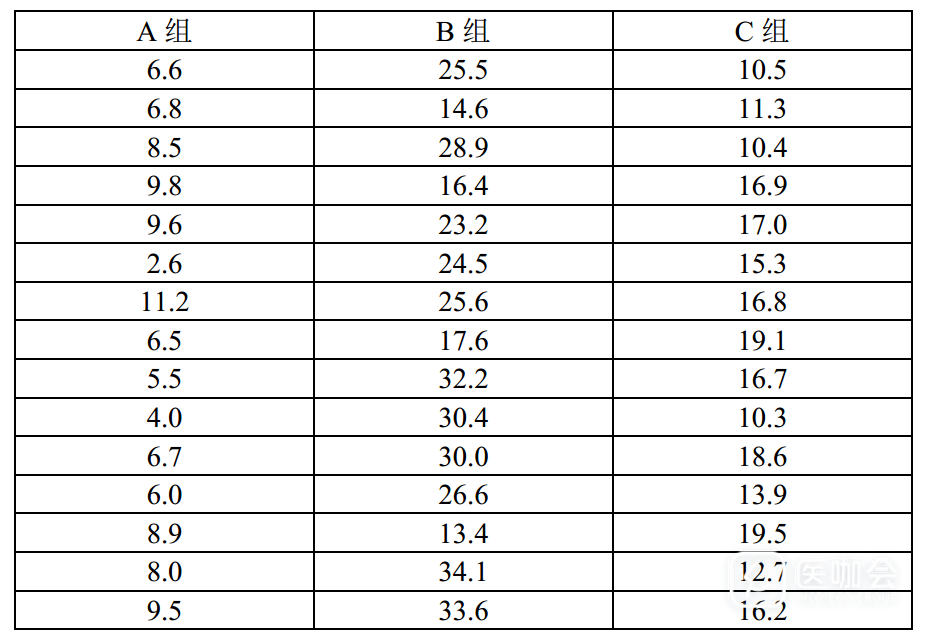
我们使用单因素方差分析中的例子:为调查A、B、C三种治疗措施对患者谷丙转氨酶(ALT)的影响,某科室将45名患者随机等分为三组,每组15人,分别采取A、B、C三种治疗措施。血常规测得治疗后ALT水平(U/L)如下。试问应用三种治疗措施后,患者的ALT水平是否有差异?
二、对问题分析
本组数据有三组患者,每组15人,测量的指标为血常规报告的ALT水平,属于多组设计的定量资料。
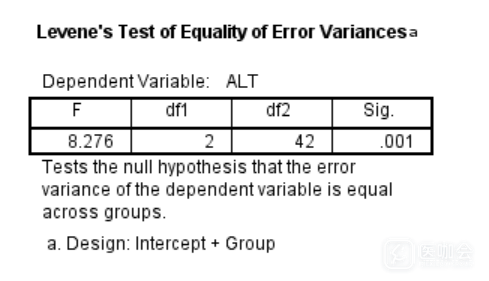
我们先进行方差齐性检验,使用单因素方差分析中的General Linear Model → Univariate,在Options中选择Homogenetity tests(方差齐性检验)。Levene’s Test of Equality of Error Variances表格报告了方差齐性检验的结果。F值=8.276,P(Sig.)=0.001<0.05,说明这三组数据方差不齐,即本组数据不满足方差分析的适应条件。因此本数据选用非参数统计方法——Kruskal-Wallis检验,它用于推断计量资料或等级资料的多个独立样本来自的多个总体分布是否有差别,检验假设H0为各组间的总体分布位置相同。



















确认删除