一、问题与数据
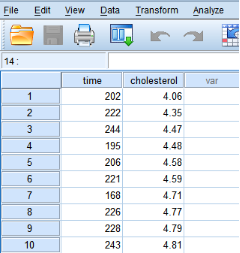
某研究者拟探讨在45岁至65岁健康男性中胆固醇浓度与久坐时间是否有关。他猜测:久坐时间较长者,血液中的胆固醇浓度要高一些。研究者收集了研究对象每天久坐时间(变量time)和胆固醇浓度(变量cholesterol)。部分数据如图1。
图1 部分数据
二、对问题分析
研究者想观察两个连续变量之间的相关性,可以使用Spearman相关(或Pearson相关)分析。Spearman相关适用于判断两个非正态分布(或者有不能剔除的异常值)的连续变量之间的相关关系。当两个连续变量均符合正态分布时,建议优先选用Pearson相关分析。
使用Spearman相关分析时,需要考虑2个假设:
假设1:观测变量是非正态分布(或者有不能剔除的异常值)的连续变量。
假设2:变量之间存在单调关系。
经分析,本研究中胆固醇浓度与久坐时间都是非正态分布的连续变量(模拟数据,假设为非正态分布),符合假设1。如何考虑和处理假设2呢?




















确认删除