本文转载自微信公众号“小白学统计”，感谢作者授权。

这篇文章主要针对临床上大家常见的一些疑问进行综合解答，全部都 以问答形式 ，快速而简要地回答这些问题，目的是提高大家对统计学方法的认识，避免一些基础错误。

1、定量资料的组间比较，一定要做正态性检验吗？

是的！

做正态性检验的目的，是要看两组数据是否分布正态。因为所有的统计方法，它的计算和检验，都是基于一定的前提条件的。比如t检验用于两组均值比较时，最终做出的统计学结论，是在数据满足正态分布这一前提下得出的。如果不满足，最后得出的结论就未必合理。

2、正态性检验结果显示P<0.05，就意味着数据不满足正态分布吗？

不一定！

大多数的统计软件中，提供四种正态性的统计学检验方法：Shapiro-Wilk（SW）检验、Kolmogorov-Smirnov（KS）检验、Cramer-vonMises（CVM）检验和Anderson-Darling（AD）检验。

这四种方法都是检验“数据满足正态性”这一原假设，所以，如果检验结果的P值小于0.05，提示可能数据不满足正态分布。

但是要记住一点，所有的假设检验都一样，数据越多，越容易推翻无效假设。换句话说， 当样本量很大的时候，即使数据看起来已经非常像正态分布了，但是检验结果也会显示P<0.05。在大样本的时候，从统计学检验结果来看，会提示你的数据永远不符合正态分布。但这并不意味着数据就不满足正态分布，只是说明后者的数据较多而已。

正因为如此，不少统计学家并不建议用统计学检验的方法来判断正态性，而是 推荐用图形等描述性方法来判断，虽然略带主观性，但考虑到多数的经典统计方法对“偏离正态”这一问题都是有一定抵抗力的，因此图形判断法还是比较有价值的。

3、标准差大于均值，就意味着不满足正态分布吗？

不一定！

大多数情况下，对于一些常规的定量资料，如身高、体重、血压值等，一般都是均值大于标准差，且表现为较为明显的正态分布。

标准差反映的是数据（围绕均值）的波动大小，如果数据波动太大，就会表现为标准差比较大。

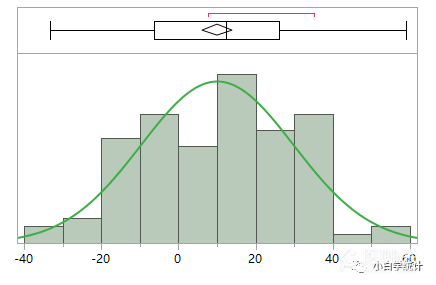
当数据明显呈偏态时，说明数据的波动较大，一般标准差会比较大。但标准差大，却不一定意味着数据一定是偏态的。比如下面的图形，该数据共100例，均值为10.05，标准差为19.7，正态性检验结果显示，P=0.29，不能拒绝“正态性”这一假定，因此仍认为这是满足正态的。

这就有一个问题：有没有一个标准，当标准差大于均值多少倍的时候，才能认为不满足正态分布？

这个就没有了。实际中主要还是自己根据数据情况，根据直方图、正态性检验等综合判断。