数据的正态性始终是困扰临床医生的一个问题，对于定量资料而言，几乎所有方法的选择都跟正态性有关。很多临床医生都很崩溃：我想直接用t检验行不行啊？可惜，正态性检验就像一个绕不过去的门槛，你恨或愤怒，它都在那里，不声不响，不悲不喜。

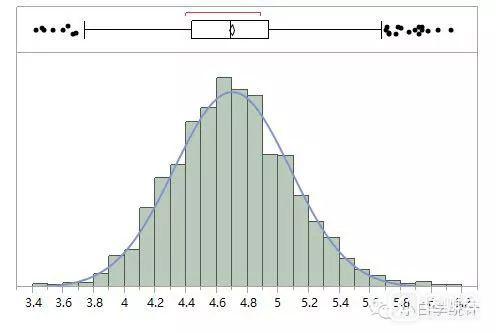
不少人对正态性检验都有一定疑问，比如看下面这个图：

你觉得这个是正态分布吗？非常接近，遗憾的是，正态性检验结果显示，不能认为是正态分布（P=0.015）。为什么会这样？明明看起来很接近了，为什么正态性检验还提示说不能认为是正态分布？

首先要明确，正态性检验的原假设是“数据服从正态分布”，如果P<0.05，拒绝原假设，即不能认为“数据服从正态分布”。也就是说，它检验的是偏离正态的程度。跟普通检验一样，这种检验也是，数据越多，越容易拒绝原假设。也就是说，同样的均值和标准差，当你有20个数据，可能是P>0.05，而200个数据时，就成了P<0.05。

听起来有点不可思议，不是说，样本量越大，越容易将它看做是正态的吗？怎么现在反而颠倒过来了，样本量越大，越不满足正态分布了。

因为正态性检验中，看的是你的数据是不是完全正态的，只要有偏离，在样本量小的时候检验不出来，而样本量大的时候，轻微偏离就会检验出来。

所以，很多统计学家其实并不是很看重正态性检验，因为，太敏感了。容不得数据有一丁点的偏离，否则就要给你显著性结果。

那么我们实际中应该怎么办？其实正常情况下，很多统计学方法，比如t检验、方差分析，虽然说前提条件是满足正态性，但并不是非常苛刻。其实所谓的满足正态，不如说是“只要不是过于偏态”更合适。也就是说，只要数据不是偏态严重，正常情况下是可以用这些方法的。

下面给临床医生介绍几种简易的判断正态性的方法（统计专业人士请绕行）：

1. 根据均值和标准差。首先，分别计算均值和标准差，然后看一下数据中有百分之多少的人在均值±1个标准差、均值±2个标准差、均值±3个标准差之内。如果分别大概是68%、95%、99%左右，说明差不多是正态的。

比如，我有10个数：

均值为0.16，标准差是1.3，那么均值±1个标准差的范围大概是-1.14和1.46，大约有7个位于这一范围（70%）。均值±1个标准差的范围大概是-2.44和2.76，大约有10个位于这一范围（100%）。比较接近68%、95%和99%，差不多可以认为是正态的。