写在前面的话：时不时有小伙伴会咨询多重线性回归、logistic回归和Cox回归的区别，本文虽不是专门讲三者区别的文章，但是文中有个表也许会对你有所帮助哦。

之前的内容里，我们介绍了在观察性研究中，当预后因素在暴露组和对照组间分布不均衡时，最简单的处理办法就是对研究资料按照混杂因素来进行分层分析，从而达到控制混杂因素的目的。

然而，分层分析仅仅适用于混杂因素较少，且多为分类变量的情况。当我们的研究中存在较多的混杂因素，且混杂因素较为复杂（例如混杂因素为多分类变量或连续变量）时，应该如何对混杂因素进行控制和调整呢？

今天我们就来一起讨论下，大家平时最常用到的多因素调整分析法。

多因素调整分析

多因素分析是相对于单因素分析而言，单因素分析仅关注一个因素在组间的差异或对结局事件的效应大小，而不考虑其他因素的影响。但实际上一种结局事件的发生和发展，常常受到多个因素的共同作用，因此仅采用单因素分析往往并不十分合理。多因素分析则是把多个变量之间的内在联系和相互影响考虑在内，同时分析多个因素对结局的影响。

在观察性研究中，我们通常可以构建一个多因素调整的回归方程，来探讨对结局有独立作用的影响因素。其中方程的因变量为结局事件，而自变量既包括研究者关注的暴露/处理因素（如药物、手术等），也包括其他可以影响结局的混杂因素（如年龄、性别、疾病严重程度等）。

三种回归模型

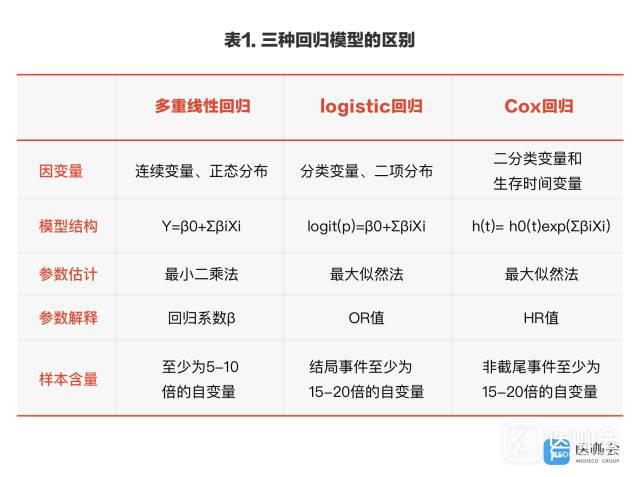
在多因素调整分析方法中，根据因变量的类型不同，我们最常应用到的三种回归模型即：多重线性回归、logistic回归及Cox回归。三种回归模型应用的条件和区别如表1所示。

需要强调的是，应用回归模型进行多因素调整时，任何回归模型都是一个黑匣子，一定要考虑到每个回归模型的使用条件及模型的稳定性，如因变量的类型、分布特点、自变量之间的独立性、共线性等问题，切忌不要盲目套用模型，以免得出错误的结果。