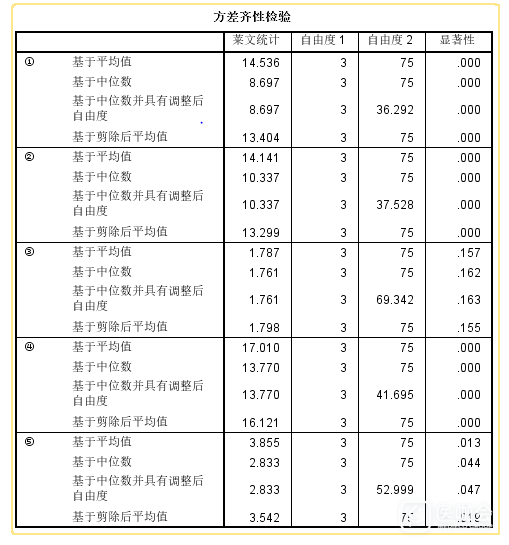
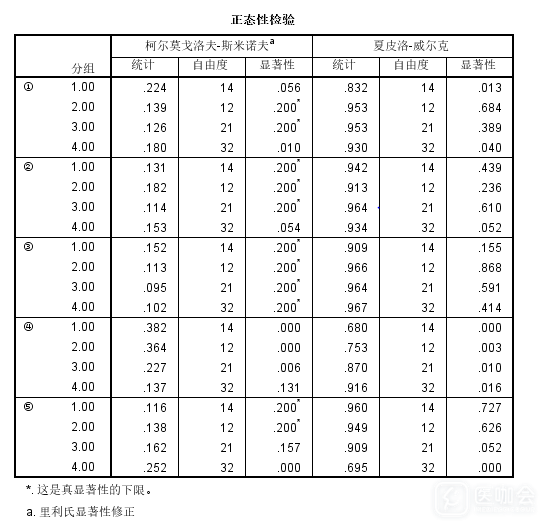
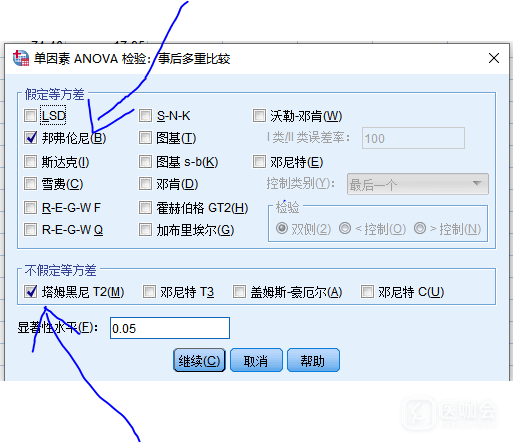
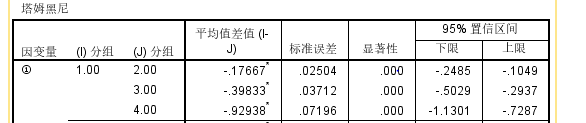
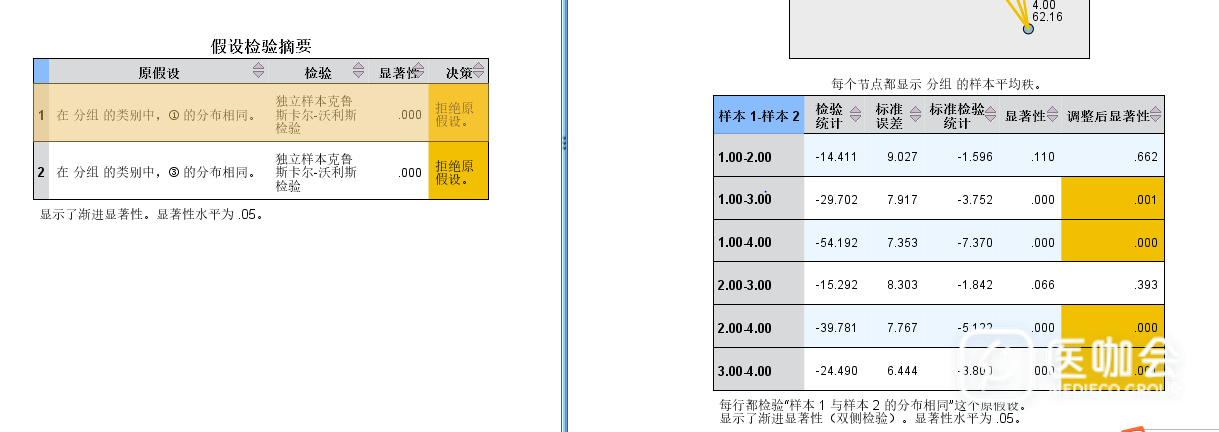
在做统计学之前，一般都需要检测这组数据是否服从正态分布与方差齐性，然后根据结果采取对应的方法或者对数据进行转换在做统计。         我现在在做四组（1-4）不同肿瘤鉴别，同时每组肿瘤都有五个指标（后面我就用①-⑤表示）需要比较差异，想做组内两两比较。         我设置了组别1-4，填好对应指标数据，然后做了一个正态分布检验和方差齐性检验，发现只有指标③完全符合了正态分布与方差齐性，我就想用单因素方差分析里面假定等方差下面的统计学方法，有人推荐选邦佛伦尼这个方法。至于指标④和⑤既不满足正态分布也不满足方差齐性，毫不犹豫选择Kruskal-Wallis检验。   但是指标①我看着结果像轻微的偏态分布（所有结果都附在图片里面），但是方差不齐；指标③服从正态分布，同样有也是方差不齐，这时我是应该严格采取Kruskal-Wallis检验，还是选择单因素方差分析里面不假定等方差下面的塔姆黑尼检验呢。         为什么我会有这种问题，因为这两种方法做出的结果不同（见图片）。我自己的认识：Kruskal-Wallis检验对数据检测是否有统计学差异主要看数据差值大小，而并不关注这两组数据是否有重叠部分。比方说，1和2组的指标①在数据上根本没有重叠的部分，但是平均值差值与其他几组间平均值差值比较是最小的，但这样看来1和2组的指标①肯定是有差异的，这时候用单因素方差里面不假定等方差下面的塔姆黑尼方法来做的结果就是p＜0.05，而如果用Kruskal-Wallis检验，组内两两比较结果则显示p远＞0.05。这样的结果如何解释。  还有几个问题，恳请懂统计的老师解答下： 正态分布检验里面的两个统计方法：柯尔莫戈洛夫-斯米诺夫与夏皮洛-威尔克一般选哪个？p＝0.040应该算是轻偏正态分布，那p＝0.01左右的还算轻度偏态分布吗？ 只服从正态分布或轻度偏正态分布但是方差不齐的能否用单因素方差分析里面不假定等方差里面塔姆黑尼检验？ 同样的问题，做两组某指标比较时候，如果只满足正态分布不满足方差齐性，到底还能不能用t检验，因为t检验结果里有一个方差齐的p值，同时也有一个方差不齐的p值；还是说只要不同时满足正态分布检验和方差齐性检验就得用Mann-Whitney检验。      研三的学生在家写毕业论文也不容易，在这里非常感谢各位老师的指点，谢谢！