一、问题与数据

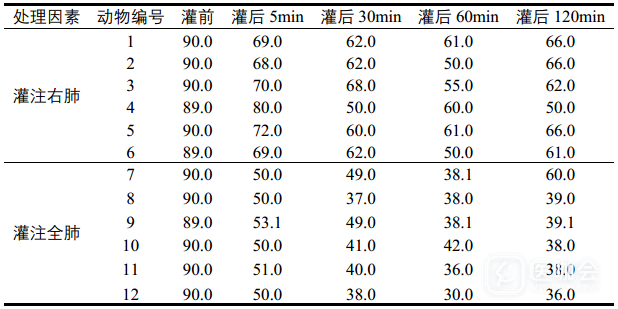
某研究者拟评估海水淹溺后残留于肺内的海水是否可导致严重的肺损伤，建立动物模型。将12只杂种犬随机分为两组，一组海水灌注右肺，另一组海水灌注全肺，每组6只。每只犬分别于海水灌注前以及灌注后5min、30min、60min、120min检测氧分压PaO2(kPa)。（案例来自于刘桂芬《医学统计学》）

试问：

（1）不同灌注处理对肺部氧分压有何作用？

（2）时间是否也会产生影响？

（3）两者之间是否存在交互作用？ 

表1. 海水灌注前后两组杂种犬的PaO2(kPa)测定结果

二、对问题分析

整个数据资料涉及两组研究对象，旨在比较两组灌注部位氧分压有无差别。与我们以往所知道的完全随机设计或者随机区组设计（研究对象被随机分配到各处理组，观察各组结局指标一次测量结果）不同，本研究对结局指标（氧分压）进行了多次测量；另外，每个观察对象在灌注前以及灌注后5min、30min、60min、120min检测的氧分压PaO2(kPa) 是相关的。这就是我们常见的重复测量设计。

由于重复测量时，每个个体的测量结果之间存在一定程度的相关，违背了方差分析数据独立性的要求，如果仍使用一般的方差分析，将会增加犯I类错误的概率，所以重复测量资料有相对应的方差分析方法。

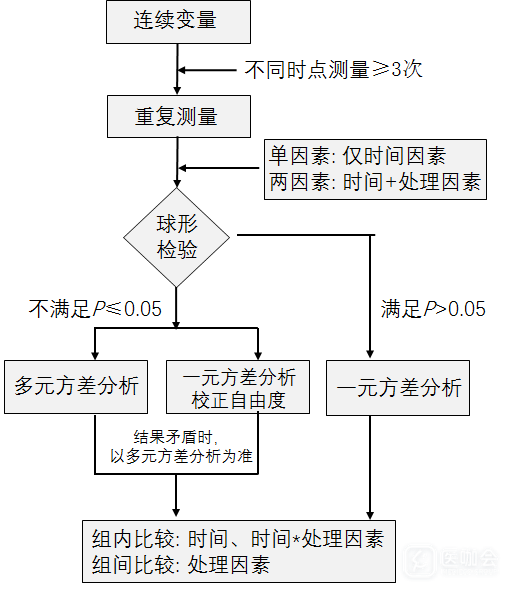
重复测量方差分析要求各时点指标变量满足球形假设(Sphericity 假设)，通常用Mauchly方法检验是否满足球形假设，若检验结果P>0.05，认为满足；若P<0.05，则不满足。当资料满足球形假设时，可直接进行一元方差分析；不满足时，应以多元方差分析结果为准（图1）。

三、SPSS操作